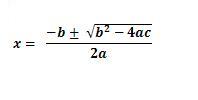COMASACA, GRADO 7 Tarde, GEOMETRÍA Per II

 

Dibuje cada una de las siguientes figuras:

1. Un cuadrado en cuyo interior haya cuatro circunferencias tangentes exteriormente y del mayor tamaño que se pueda.

2. Un rectángulo de 10 cm. por 4cm. con el mayor cuadrado en su interior, tal que dos de sus vértices no consecutivos se encuentren en dos de los lados opuestos del rectángulo.

3. Una circunferencia con cuatro circunferencias en su interior, las de mayor radio, todas que se toquen externamente y toquen internamente a la grande.

4. Dos circunferencias, una de radio 5cm y la otra de 3cm, tal que sean tangentes externas y enciérrelas con un triángulo que toque a ambas, a la grande en tres puntos y a la pequeña en dos puntos.

5. Se quiere bordear con una cinta de color rojo, una mesa de color verde de radio 2 metros. Si la mesa es de forma circular, ¿qué cantidad de cinta es necesaria?

 

6. Consulte en internet cuál es la longitud de la distancia de la Tierra al Sol y con este dato calcule la longitud de la trayectoria de nuestro planeta alrededor de esta estrella.

 

7. Consulte en internet cuál es la distancia de la Tierra a la Luna y suponga que esta sigue una trayectoria circular. ¿Qué distancia recorre nuestro satélite en un día?

COMASACA, GRADO 9°Mañ, Matemáticas, Taller Final

Recordemos los ejes temáticos más importantes de los tres periodos en este año lectivo 2010 – 2011:

I Función Lineal

II Sistemas de ecuaciones lineales

III Función cuadrática

Propósitos del taller:

Afectivo: mostrar interés por la exploración matemática desde la solución a problemas en los que aplica los conocimientos y habilidades adquiridos durante el año.

Cognitivo: hacer uso de la lógica matemática y las estructuras mentales aprehendidas para dar solución a las actividades propuestas.

Expresivo: hacer uso del lenguaje matemático para construir las soluciones a los problemas planteados y darlas a conocer de manera clara y precisa.

Modo de presentación del taller:

Lo deben presentar en hojas cuadriculadas tamaño oficio o carta. Debe aparecer la pregunta a lapicero o impresa y seguida la respuesta a lápiz. Si existe un gráfico o imagen, debe aparecer en el taller.

TALLER

1. Sea el conjunto A={1,2,3,4,5,6} y B={0,1,2,3}, escribir los elementos del conjunto C, conformado por todas la parejas ordenadas (a,b), donde a pertence a A y b pertence a B, tales que el elemento a se divisor del elemento b. Por ejemplo la pareja (2,2)  sirve ya que 2 divide exactamente al 2.

2. Sea el conjunto A={1,2,3,4,5,6} y B={0,1,2,3}, escribir los elementos del conjunto C, conformado por todas la parejas ordenadas (a,b), donde a pertence a A y b pertence a B, tales que el elemento a sea menor que el elemento b.

3. Sea el conjunto A={1,2,3,4,5,6} y B={0,1,2,3,6}, escribir los elementos del conjunto C, conformado por todas la parejas ordenadas (a,b), donde a pertence a A y b pertence a B, tales que el elemento b sea mayor que el elemento a.

4. Sea el conjunto A={1,2,3,4,5,6} y B={0,1,2,3}, escribir los elementos del conjunto C, conformado por todas la parejas ordenadas (a,b), donde a pertence a A y b pertence a B, tales que el elemento a sea equivalente al elemento b.

5. Sea el conjunto A={1,3,4,6} y B={0,1,2,3}, escribir los elemnentos del conjunto C=AxB.

6. Sea el conjunto A={3,4,6}, B={0,1,2,3} y C=AxB,  escribir los elemnentos del conjunto C tal que sus componentes sean equivalentes.

7. Indicar cuál de las siguientes relaciones es reflexiva:

a) {(1,1), (2,2), (1,2), (2,1), (3,3), (3,1)}

b) {(1,1), (2,2), (1,2), (2,1), (3,1)}

8. En una relación simétríca se cumple que para todo (a,b) existe:

a) (a,a)                       b)  (b,b)                   c) (b,a)

9. En una relación transitiva se cumple que para todo (a,b) y (b,c) que pertenecen ala relación,  existe:

a) (a,c)                       b)  (a,b)                   c) (b,a)

10. Complete el párrafo donde se define función matemática:

«una función matemática es una _____________ entre dos conjuntos X, Y tales que a cada elemento del conjunto X, llamado _______, le corresponde uno y solamente un elemento del conjunto Y llamado ___________».

11. Una función f: X->Y, está definida mediante la regla de asignación y=2x-1. El dominio de f está formado por los elementos del conjunto X={-2,-1,0,1} y Y={-7,-6,..+4,+5}. Escribir su rango.

12. Una función f: X->Y, está definida mediante la regla de asignación y=2x-6. El dominio de f está formado por los elementos del conjunto X={-2,-1,0,1} y Y={-10,-9,..-4,-3}. Escribir su rango.

13. Una función f se representa en un diagrama sagital, tal como se muestra en la figura.

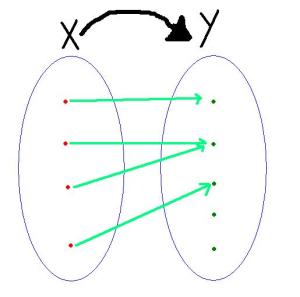
Clasifique f como inyectiva, sobreyectiva o biyectiva. Justificar su respuesta.

14. ¿Cuál o cuáles de las asignaciones a, b, c, d, o e se deben suprimir para que la relación de la gráfica sea función? Justificar la respuesta.

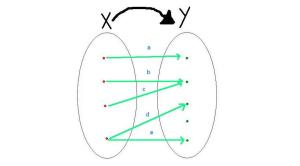
Diagrama sagital que representa la correspondencia entre los elementos del conjunto X con los elementos del conjunto Y.

a) a o b                     b) b y e                    c)  d  o e                d) sólo e

15. Los elementos de una relación R son : (1,1), (2,3), (1,2) y (3,3), teniendo como conjunto de partida a A= {1,2,3} y de llegada B={1,2,3,4}. ¿ Es R una función?

16. ¿Qué se puede concluir en una función, si se descubre que las parejas (a,b) y (c,d) cumplen que a=c? Apóyese en un diagrama sagital para la respuesta.

17. ¿Qué se puede concluir en una función, si se descubre que las parejas (a,b) y (c,d) cumplen que b=d? Apóyese en un diagrama sagital para la respuesta.

18. ¿Cuál o cuáles de los puntos a, b, c, d, e o f debe(n) suprimirse para que la relación se convierta en función? Escriba todas las posibles opciones de suprimir puntos o pares de puntos.

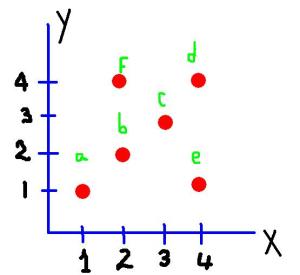
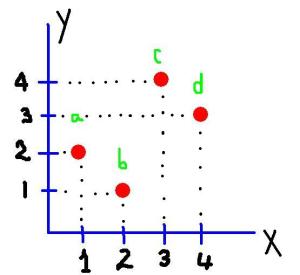
19. ¿En qué lugar ubicaría usted el punto d para que la función deje de ser inyectiva, según la gráfica de abajo? Apóyese en un diagrama sagital para justificar su respuesta.

20. Represente en el plano cartesiano algunas parejas ordenadas (x,y) tal que y=x.

21. Represente en el plano cartesiano algunas parejas ordenadas (x,y) tal que y=2x.

22. Represente en el plano cartesiano algunas parejas ordenadas (x,y) tal que y=-x.

23. Represente en el plano cartesiano algunas parejas ordenadas (x,y) tal que x+y=0.

Solución:

Para identificar números que sumados den cero, se debe poner una variable en función de la otra, así resulta más cómodo. Escribiendo y en función de x (lo más común) se obtiene:

x+y=0

y=0-x

y=-x

Haciendo una tabulación y graficando, se obtiene:

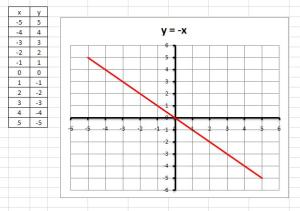
Grafica de la función lineal y=-x. Nótese que tiene pendiente negativa.

24. Represente en el plano cartesiano algunas parejas ordenadas (x,y) tal que x-y=0.

25. Represente en el plano cartesiano algunas parejas ordenadas (x,y) tal que y=2x-1.

26. Represente en el plano cartesiano algunas parejas ordenadas (x,y) tal que 2x-y=1.  Compárala con la del ejercicio 25.

27. Represente en el plano cartesiano algunas parejas ordenadas (x,y) tal que y=x-10.

28. Represente en el plano cartesiano algunas parejas ordenadas (x,y) tal que 2x-3y=12.

29. Represente en el mismo cartesiano las rectas de ecuación y=x   y    y=-x. ¿dónde se cruzan?

30. Represente en el mismo cartesiano las rectas de ecuación y=x   y    y=2x-1. ¿dónde se cruzan?

31. Buscar dos números que sumados den 75, tal que el uno sea las dos terceras partes del otro. Plantear ecuaciones.

32. En una alcancía hay $21.000 entre monedas de 200 y 500. Si hay 63 monedas, ¿cuántas monedas hay de cada tipo?

34. Resolver por el método de eliminación:

3x+y=2

-2x+y=-1

35. Resolver por el método de sustitución:

2x-3y=5

4x-y=35

36. Resolver por el método de igualación:

3(x+y)=2

10=2(x-3y)

37. Resolver por determinantes:

1/x  + 1/y=10

3/x –  2/y=-8

38. Represente en el plano cartesiano el área A en función de su altura h, de un triángulo cuya base mide 5cm.

39. Represente en el plano cartesiano el perímetro P de un rectángulo en función de su largo l, si su ancho mide 10cm.

40. Represente el área A de un rectángulo en función de su largo L si su ancho mide 4cm.

41. Represente el área A de un círculo en función de su radio r.

42. Represente el área A de un pentágono en función de la longitud L de su lado.

43. Represente el área A de un hexágono en función de la longitud L de su lado.

44. Represente el área A de un heptágono en función de la longitud L de su lado.

45. El lado de un triángulo equilátero mide 10 cm. Calcular la longitud de su altura.

46. Una piscina rectángular tiene dimensiones 4mx3mx10m. ¿Qué cantidad máxima de agua le cabe?

47. Calcular el volumen de un cubo cuya arista mide 4cm.

48. Un tetraedro tiene por arista 5cm, caclular su área total y volumen.

49. Calcular el área total y volumen de un cilindro de radio 4m y altura 8m.

50. Una máquina llena un recipiente cónico de 10m de alto y 4m de radio a razón de 5m³ por minuto. ¿Cuánto tiempo tarda en llenarlo?

51. Despeje x en la ecuación x²-4=0

52. Despeje x en la ecuación x²+4=0

53. Despeje x en la ecuación x²-9=0

54. Despeje x en la ecuación x²+9=0

55. Despeje x en la ecuación x²+2x-8=0

56. Despeje x en la ecuación x²+2x-15=0

57. Despeje x en la ecuación x²+4x=32

58. Despeje x en la ecuación x(x-1)=0

59. Despeje x en la ecuación x(x+1)=0

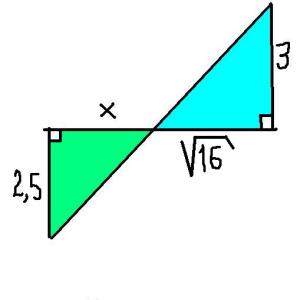
60. Despeje x en la ecuación 2x(10-5x)=0

61. Graficar y=x²

62. Graficar y=x²-5

63. Graficar y=x²+5

64. Escriba las semejanzas y diferencias entre las graficas 62 y 63.

65. Graficar y=-x²

66. Escriba las semejanzas y diferencia entre las gráficas 61 y 65

67. Graficar y= x²-2x

68. Graficar y= x²+2x

69. Comparar las gráficas 67 y 68, ¿qué concluyes?

70. Graficar y=(x-1)²+6

71. Graficar y=(x-1)²-6

72. Compare 70 con 71

73. Escriba la ecuación y=x²+4x-10 de la forma y-k=(x-h)² e identifique el vértice de componentes (h,k).

74. Escriba la ecuación y=x²-8x-84  de la forma y-k=(x-h)² e identifique el vértice de componentes (h,k).

75. Calcular: √4 + √9

76. Calcular: √4 – √9

77. Calcular: 2√4 + √9

78. Calcular: √4 + 5√9

79. Calcular: (√4)² + (√9)²

80. Calcular: √16 – √81

Solución:

√16 – √81

4-9

-5

81. Calcular: (√4)²+2 √4√9+ (√9)²

82. Calcular: (√2)²+2 √2√3+ (√3)²

83. Calcular: (√5)²-2 √5√6+ (√6)²

84. Calcular: (√-4)²+2 √-4√9+ (√9)²

85. Calcular:  √2 + √8 + √32

Solución

√2 + √8 + √32

=√2 + √4(2) + √16(2)

=√2 + √4√(2) + √16√(2)

=1√2 + 2√(2) + 4√(2)

=(1+2+4)√2

=7√2

86. Calcular:  √3 + √12 + √48

87. Calcular:  -10√27 +5 √300 + 5

88. Calcular:  √2( √8 + √3)

89. Calcular:  √5(√2 + √10)

Solución:

√5(√2 + √10)

√5√2 +√5 √10)

√10 + √50

√10 + √25(2)

√10 + √25√2

√10 + 5√2

Nótese que el 10 no tiene factores que tengan raíz cuadrada exacat, por eso no se simplifica.

90. Calcular:  (√2 – √3)²

91. Calcular:  (√2)²-2(√2)(√3) + (√3)²

92. Compare 90 con 91, ¿qué concluyes?

93. Calcular 4/√3

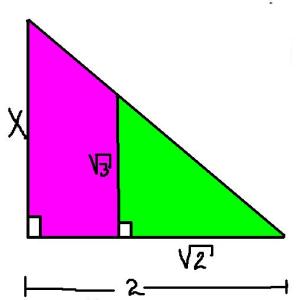
94. Calcular el valor de x según el dibujo:

95. Calcular el valor de x según el dibujo:

96. Calcular el valor de x según el dibujo:

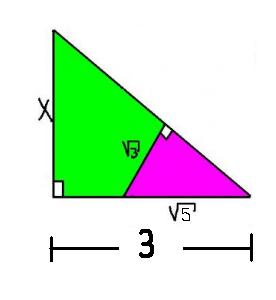
97. Calcular el valor de x según el dibujo:

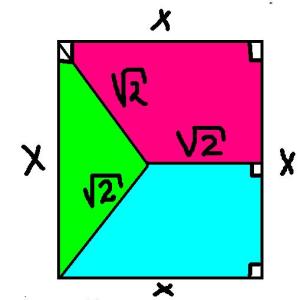98 . Calcular el valor de x según el dibujo:

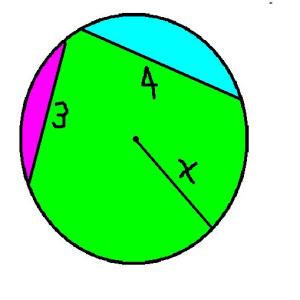99. A una fiesta entran 30 personas que se saludan todas entre sí y una sola vez. ¿cuántos saludos hubo?

100. Una tómbola consiste en ingresar a una urna los números del 0 al 999 y hacer que cada uno de los 1000 participantes saquen un número, el cual deben pagar en dinero así: si el número es de una sola cifra paga la cantidad multiplicada por 1000, si es de dos cifras paga la cantidad multiplicada por 10 y si es de tres cifras paga la cantidad multiplicada por 1. ¿Cuánto dinero se recoge en la tómbola?

Comasaca Tarde, Grado 11, Caracterizando Gráficas de funciones matemáticas.

Hasta el momento hemos observado como caracterizar funciones polinómicas y funciones racionales. Recordemos lo socializado en clase acerca de las seis gráficas qeu sirvieron para calcular los límites:

Desarrollo:

1.

COMASACA, Grado 9 Mañana, Conjuntos Numéricos

Imagen tomada de la Guía de 9°, Arquidiócesis de Cali, Colegio Mayor Santiago de Cali 2011.

Hemos visto cómo al realizar el trazado de las gráficas de una función cuadrática, cuya forma es:

y=ax²+bx+c

… nos topamos con el cálculo de sus cortes con el eje x, de donde se desprende la solución a una ecuación cuadrática de la forma:

0=ax²+bx+c

… que implica el calcular un raíz cuadrada de la forma:

Fórmula que permite calcular el valor de x en la ecuación 0=ax²+bx+c.

Por ejemplo, al graficar la función:

y=x²-4x-5, se obtiene:

1. Se identifican los coeficientes a, b y c que son:

y=1x²-4x-5

a=1

b=-4

c=-5

Como a=1 y 1>0, la parábola se abre hacia arriba y debe tener un punto mínimo.

2. Se calcula el corte con el eje y haciendo x=0 así:

y=0²-4(0) -5

y=0-0-5

y=-5

o sea que corta al eje y en el punto (0,5)

3. Se calculan los cortes con el eje x, haciendo y=0, así:

y=x²-4x-5

0=x²-4x-5

x²-4x-5=0

x²-4x+(-4/2)²=5+(-4/2)²

x²-4x+(-2)²=5+(-2)²

x²-4x+4=5+4

(x-2)²=9

Es aquí donde se debe calcular una raiz cuadrada, en este caso para el 9, que resultó ser una cantidad positiva, puesto que si hubiera sido -9, la raíz cuadrada de -9 no exite en los números reales y hubiera sido necesario acudir al conjunto de los números complejos. Siguiendo con el proceso:

x-2=±√9

x=2±3

de donde se obtienen dos valores, uno con la raíz cuadrada positiva y otro con la raíz cuadrada negativa:

X1=2+3     ó      X2=2-3

X1=5     ó      X2=-1

Significa que corta al eje x en dos puntos:

Primer corte en (-1,0) y segundo corte en (5,0)

En verde aparecen los puntos de corte con el eje X.

4. Cálculo del punto mínimo o vértice de la parábola.

Cómo la parábola es vertical, los puntos de corte con el eje x equidistan del punto central por donde pasa el eje de simetría, en este caso por el 2:

ya que el 2 está a tres unidades del 5 y también a tres unidades del -1.Se debe entonces reemplazar en la ecuación

y=x²-4x-5

la x por 2 o sea  x=2:

y=(2)²-4(2)-5

y=4-8-5

y=4-13

y=-9

Significa que el vértice está en (2,-9) que efectivamente es el valor que se muestra en la imagen de arriba. Pero, el haber obtenido x=2 por símple inspección deja dudas sobre la precisión en aquellos casos donde no es tan facil, a simple vista, dar con el valor medio de los cortes con x, para esto se debe escribir la ecuación y=x²-4x-5 en la forma:

y-k=(x-h)²

De tal manera que si la parte que está al cuadrado se hace cero, se obtiene el valor mínimo de la expresión cuya coordenada es (h,k). Veamos:

y=x²-4x-5

y=x²-4x-5

y=x²-4x-5

y=x²-4x+(-4/2)²-(-4/2)²-5

y=x²-4x+(-2)²-(-2)²-5

y=x²-4x+4-4-5

y=(x-2)²-9

y+9=(x-2)²

de aquí se obtiene que h=+2 y k=-9

(se toman con los valores contrarios en signo)

Nótese que si x=2, el cuadrado (x-2) se hace nulo y el valor de y es -9, que serían las coponentes de las coordenadas del vértice.

Veamos ahora qué sucede si la función cambia a:

y=x²-4x+5

Enfoquemos la atenión sólo en los cortes con el eje x:

Completando el trinomio para que sea cuadrado perfecto, se tiene que:

y=x²-4x+4-4+5

Nótese que el valor que lo completa es el 4

y=(x-2)²+1

haciendo y=0 se tiene que

0=(x-2)²+1

0-1=(x-2)²

-1=(x-2)²

(x-2)²=-1

x-2=±√-1

como √-1 no existe en  el conjunto de los números reales, acudimos al conjunto de los números complejos, donde defines a √-1=i, reemplazando se tiene que:

x=2±i

de donde se obtienen dos soluciones complejas:

X1=2+i     ó  X2=2-i

Que significa la grafica de la función no corta al eje x. Observa la grafica de abajo:

Concentraremos nuestra atención en este tipo de radicales donde la cantidad subradical es negativa y el índice es par.

Recuerda que:

Según la imágen, el 4 es el índice radical y el 16 es la cantidad subradical. Su resultado es 2 ya que 2 elevado a la 4 da como resultado 16, pero también lo és -2 ya que:

(-2)(-2)(-2)(-2)=+16

entonces:

Pero para el caso:

No tendría solución en lo números reales ya que NO existe ningún número real que al elevarlo al cuadrado dé como resultado un valor negativo y se debe expresar en términos de i (cantidad que expresa un valor imaginario), así:

La respuesta es 4i.

Nótese que en el mentefacto inicial de este artículo, aparece como característica esencial de los números reales el que al elevar un número real al cuadrado, se obtiene siempre una catidad positiva, situación que NO sucede con los números complejos, pues si se elva 4i al cuadrado, se obtiene una cantidad negativa, veamos:

(4i)²

=4² i²

=16 i²

=16(√-1)²

=16(-1)

=-16

Esto implica que se deban realizar operaciones con expresiones imaginarias, propias del conjunto de los números complejos.

Actividad.

I. Calcular los punto de corte de la grafica de la ecuación de cada una de las siguientes parábolas, haciendo uso, según el caso, del conjunto de los números complejos. También graficar.

1.      y= x²+12x+40

2.      y=x²-10x+41

3.      y=2x²-28x+108

II. Calcular:

1. √4

2. √16

3.  ±√25

4. -√36

5. √100

6. √4 + √49

7. (1-√4) (2√81-√169)

8. (√4)²

9. √(5²)

10.  √(3²+4²)

11. √-4

12.   1-√-9

13.  √2+√8

14.  √12 + √27

15. Exprese 72 como un producto donde mínimo uno de sus factores tenga raíz cuadrada exacta.

16. Exprese 27 como un producto donde mínimo uno de sus factores tenga raíz cuadrada exacta.

17. Exprese 32 como un producto donde mínimo uno de sus factores tenga raíz cúbica exacta.

18.  f(√3) si f(x)= x²-3x+1.

19. f(√-4) si f(x)= x²-3x+1.

20. 2√5 (3√5)

21. 4(2√7-3√5)

22. (1+√2) (1-√2)

23. √√16

24. √50-√18

25. 3√2+4√2-60√2