Hemos visto cómo al realizar el trazado de las gráficas de una función cuadrática, cuya forma es:
y=ax²+bx+c
… nos topamos con el cálculo de sus cortes con el eje x, de donde se desprende la solución a una ecuación cuadrática de la forma:
0=ax²+bx+c
… que implica el calcular un raíz cuadrada de la forma:
Por ejemplo, al graficar la función:
y=x²-4x-5, se obtiene:
1. Se identifican los coeficientes a, b y c que son:
y=1x²-4x-5
a=1
b=-4
c=-5
Como a=1 y 1>0, la parábola se abre hacia arriba y debe tener un punto mínimo.
2. Se calcula el corte con el eje y haciendo x=0 así:
y=0²-4(0) -5
y=0-0-5
o sea que corta al eje y en el punto (0,5)
3. Se calculan los cortes con el eje x, haciendo y=0, así:
y=x²-4x-5
0=x²-4x-5
x²-4x-5=0
x²-4x+(-4/2)²=5+(-4/2)²
x²-4x+(-2)²=5+(-2)²
x²-4x+4=5+4
(x-2)²=9
Es aquí donde se debe calcular una raiz cuadrada, en este caso para el 9, que resultó ser una cantidad positiva, puesto que si hubiera sido -9, la raíz cuadrada de -9 no exite en los números reales y hubiera sido necesario acudir al conjunto de los números complejos. Siguiendo con el proceso:
x-2=±√9
x=2±3
de donde se obtienen dos valores, uno con la raíz cuadrada positiva y otro con la raíz cuadrada negativa:
X1=2+3 ó X2=2-3
X1=5 ó X2=-1
Significa que corta al eje x en dos puntos:
Primer corte en (-1,0) y segundo corte en (5,0)
4. Cálculo del punto mínimo o vértice de la parábola.
Cómo la parábola es vertical, los puntos de corte con el eje x equidistan del punto central por donde pasa el eje de simetría, en este caso por el 2:
ya que el 2 está a tres unidades del 5 y también a tres unidades del -1.Se debe entonces reemplazar en la ecuación
y=x²-4x-5
la x por 2 o sea x=2:
y=(2)²-4(2)-5
y=4-8-5
y=4-13
y=-9
Significa que el vértice está en (2,-9) que efectivamente es el valor que se muestra en la imagen de arriba. Pero, el haber obtenido x=2 por símple inspección deja dudas sobre la precisión en aquellos casos donde no es tan facil, a simple vista, dar con el valor medio de los cortes con x, para esto se debe escribir la ecuación y=x²-4x-5 en la forma:
y-k=(x-h)²
De tal manera que si la parte que está al cuadrado se hace cero, se obtiene el valor mínimo de la expresión cuya coordenada es (h,k). Veamos:
y=x²-4x-5
y=x²-4x-5
y=x²-4x-5
y=x²-4x+(-4/2)²-(-4/2)²-5
y=x²-4x+(-2)²-(-2)²-5
y=x²-4x+4-4-5
y=(x-2)²-9
y+9=(x-2)²
de aquí se obtiene que h=+2 y k=-9
(se toman con los valores contrarios en signo)
Nótese que si x=2, el cuadrado (x-2) se hace nulo y el valor de y es -9, que serían las coponentes de las coordenadas del vértice.
Veamos ahora qué sucede si la función cambia a:
y=x²-4x+5
Enfoquemos la atenión sólo en los cortes con el eje x:
Completando el trinomio para que sea cuadrado perfecto, se tiene que:
y=x²-4x+4-4+5
Nótese que el valor que lo completa es el 4
y=(x-2)²+1
haciendo y=0 se tiene que
0=(x-2)²+1
0-1=(x-2)²
-1=(x-2)²
(x-2)²=-1
x-2=±√-1
como √-1 no existe en el conjunto de los números reales, acudimos al conjunto de los números complejos, donde defines a √-1=i, reemplazando se tiene que:
x=2±i
de donde se obtienen dos soluciones complejas:
X1=2+i ó X2=2-i
Que significa la grafica de la función no corta al eje x. Observa la grafica de abajo:
Concentraremos nuestra atención en este tipo de radicales donde la cantidad subradical es negativa y el índice es par.
Recuerda que:
 Según la imágen, el 4 es el índice radical y el 16 es la cantidad subradical. Su resultado es 2 ya que 2 elevado a la 4 da como resultado 16, pero también lo és -2 ya que:
Según la imágen, el 4 es el índice radical y el 16 es la cantidad subradical. Su resultado es 2 ya que 2 elevado a la 4 da como resultado 16, pero también lo és -2 ya que:
(-2)(-2)(-2)(-2)=+16
entonces:
Pero para el caso:
No tendría solución en lo números reales ya que NO existe ningún número real que al elevarlo al cuadrado dé como resultado un valor negativo y se debe expresar en términos de i (cantidad que expresa un valor imaginario), así:
Nótese que en el mentefacto inicial de este artículo, aparece como característica esencial de los números reales el que al elevar un número real al cuadrado, se obtiene siempre una catidad positiva, situación que NO sucede con los números complejos, pues si se elva 4i al cuadrado, se obtiene una cantidad negativa, veamos:
(4i)²
=4² i²
=16 i²
=16(√-1)²
=16(-1)
=-16
Esto implica que se deban realizar operaciones con expresiones imaginarias, propias del conjunto de los números complejos.
Actividad.
I. Calcular los punto de corte de la grafica de la ecuación de cada una de las siguientes parábolas, haciendo uso, según el caso, del conjunto de los números complejos. También graficar.
1. y= x²+12x+40
2. y=x²-10x+41
3. y=2x²-28x+108
II. Calcular:
1. √4
2. √16
3. ±√25
4. -√36
5. √100
6. √4 + √49
7. (1-√4) (2√81-√169)
8. (√4)²
9. √(5²)
10. √(3²+4²)
11. √-4
12. 1-√-9
13. √2+√8
14. √12 + √27
15. Exprese 72 como un producto donde mínimo uno de sus factores tenga raíz cuadrada exacta.
16. Exprese 27 como un producto donde mínimo uno de sus factores tenga raíz cuadrada exacta.
17. Exprese 32 como un producto donde mínimo uno de sus factores tenga raíz cúbica exacta.
18. f(√3) si f(x)= x²-3x+1.
19. f(√-4) si f(x)= x²-3x+1.
20. 2√5 (3√5)
21. 4(2√7-3√5)
22. (1+√2) (1-√2)
23. √√16
24. √50-√18
25. 3√2+4√2-60√2


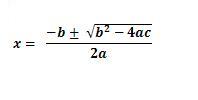







me puedes decir cual es la respuesta de la pregunta 13.
Hola, debes simplificar la raiz cuadrada de 8 que es equivalente a 2 por la raíz cuadrada de 2 o sea
raiz 8 + raiz 2
2 raiz2 + 1 raiz 2
=3raiz 2